并行计算复习课
复习课
第一章 Amdal 定律 对定律的理解(任务不变的情况下,速度的提升、加速比)、加速的极限
应用题 6’*5
网格和线程块的布局,计算全局id
并行、并发、线程束、全局id、CPU多核与GPU众核
程序分析题 10*2
给代码写结果、分析为什么会有这种结果
CPU多核 10*2
数据划分:明确每个部分处理的数据范围
任务并行:线程池实验
CUDA编程 15*2
具体的问题,设计网格与线程块,或者给了线程块,只需要设计网格;
主函数中的固定流程;关键在写核函数;
并行计算
并发与并行
串行:单机单核,指令顺序执行。
并发:单机单核,指令在时间上并行执行,同一时间间隔发生。
并行:单机多核,多机单/多核,指令在空间上并行,同一时刻发生。
并行计算就是在并行计算机或者分布式系统等高性能计算系统上做的超级计算。并行计算可以降低单个问题求解的时间,增加求解规模与精度,提高吞吐率等。
三种分类:
计算模式:时间并行(流水线)、空间并行(多处理器)
程序逻辑:任务并行、数据并行
应用角度:计算密集、数据密集、网络密集
Flynn分类法
依据指令流(instruction stream)和数据流(data stream)的执行方式对并行计算机体系结构分类的一种方法。
包含SISD(早期串行机),SIMD(单核计算机),MISD(很少用),MIMD(多核计算机,并行);
Amdahl定律
假定任务数量一定,通过计算性能加速比,揭示了一个程序中无法并行化的部分会限制整个程序的性能提升的规律。
$$S=\frac{W_{s}+W_{p}}{W_{s}+W_{p}/p}$$
其中$W_{s}$为串行任务数量,$W_{p}$为并行任务数量,$p$为处理器数目,$S$为加速比。
依据串行分量的占比$f=W_{s}/W$,将上式同时除以$W$可得下面的式子:
$$S=\frac{f+(1-f)}{f+\frac{1-f}{p}} =\frac{p}{1+f(p-1)}$$
$\lim_{x\rightarrow \infty}S=1/f$,当处理器的数目无限增大时,系统能达到的加速比受制于程序中的串行部分。
1.一个串行应用程序中,有20%的比例必须串行执行,现在需要实现3倍的性能提升,为实现这个目标,需要多少个CPU?如果要实现5倍的加速比,需要多少个CPU?
2.一个运行在5个计算机上的并行程序,有10%的并行部分。相对于在一个计算机上的串行执行,加速比是多少?如果我们想将加速比提升2倍,需要多少个CPU?
3.将一个不可并行部分占5%的应用程序修改为并行程序。目前市场上有两种并行计算机:计算机X有4个CPU,每个CPU可以在1个小时内完成该应用程序的执行;计算机Y有16个CPU,每个CPU可以在2个小时内执行完该应用程序。如果需要最小化运行时间,请问你该买哪个计算机?CUDA概述
异构计算
GPU的并行计算是一种异构计算,分为主机端(CPU)和设备端(GPU),二者关系从来都不是平等的,CUDA甚至需要明确标识代码需要在哪运行。
CPU和GPU的差异
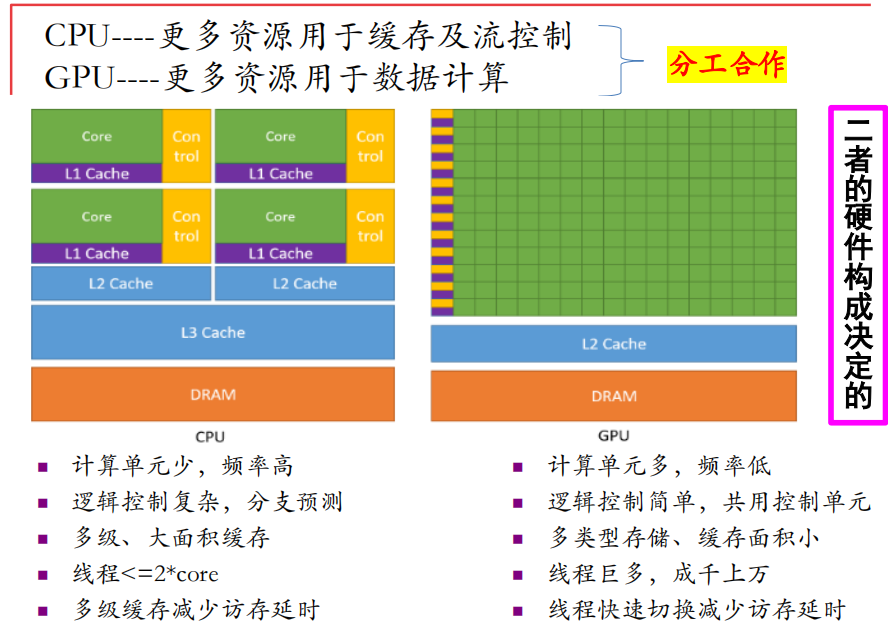
直观来说,CPU更多资源用于缓存与控制流,GPU则是更多的数据计算。
- 在GPU环境下,GPU的核心负责所有计算任务的执行,但工作指令总是来自CPU。
- 在GPU情况下,GPU核心从不自己获取数据,数据总是来自CPU端,计算结果再传回CPU端。因此,GPU在后台只是扮演计算加速器的角色,为CPU完成某些外包任务。
- 这种类型的体系架构只有在有着大量的并行处理单元,而不是仅有2个或4个时,才会非常有效。
- 线程束的概念对GPU的体系结构有重大影响。数据必须以同样大小的数据块为单位输入GPU,数据块是半个线程束,即16个元素。
- 数据必须以半个线程束的大小传输给GPU核心的事实意味着负责将数据传入GPU的存储系统应该每次输入16个数据。这需要一次能够传输16个数的并行存储子系统。这就是为什么GPU的DRAM存储器是由DDR5构成的,因为它是并行存储器。
- 由于GPU核心和CPU核心是完全不同的处理单元,因此可以预见它们具有不同的ISA(指令集架构)。即:它们说的是不同的语言。
GPU线程与CPU线程也有所不同,创建开销极低。CPU通过多级cache缩减延迟,而GPU是通过流水线提高吞吐量来缩减延迟的。
由于其设计目标的不同,CPU需要很强的通用性来处理各种不同的数据类型,同时逻辑判断又会引入大量的分支跳转和中断的处理。而GPU面对的则是类型统一的、相互无依赖的大规模数据和不需要被打断的纯净的计算环境。
CUDA线程组织形式
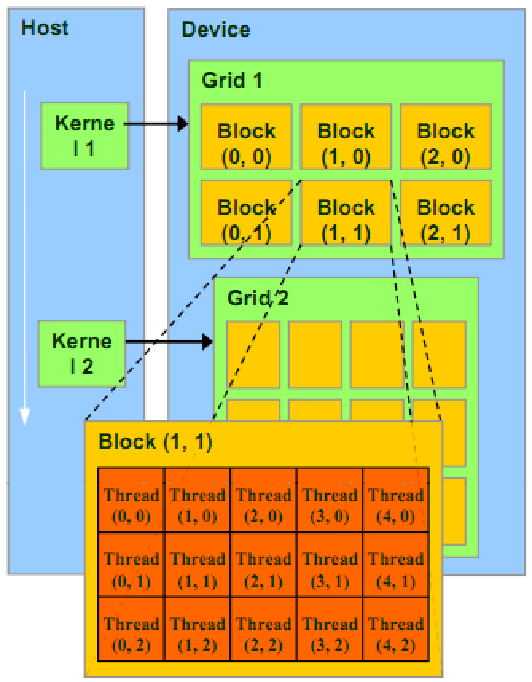
Thread:并行的基本单位
Thread Block:互相合作的线程组
允许彼此同步
通过快速共享内存交换数据
以1维、2维或3维组织
最多包含1024个线程
Grid:一组线程块
以1维、2维组织,也可3维
共享全局变量
Kernel:在GPU上执行的核心程序
One kernel One Grid
CUDA主机/设备编程模型
函数限界符
- _ device _:在device端执行,并且也只能从device端调用,即作为device端的子函数来使用。
- _ host _:在host端执行,也只能从host端调用,与一般的C函数相同。不可以和__global__同时用,但可和__device__,此时函数会在device和host都编译。
- _ global _ :即kernel函数,它在设备上执行,但是要从host端调用。
CUDA核函数的限制
- 只能访问设备内存
- 必须返回void类型
- 不支持可变数量的参数
- 不支持静态变量
- 显示异步行为,意味着host不会等待kernel执行完就执行下一步
并行计算模型SIMT
线程块是程序启动的基本单位,线程束是程序执行的单位;
例如,我们说一个块大小是256个线程时,也就是意味着线程块大小为8个线程束。每个线程束总是包含32个线程。这个参数表明:虽然启动程序时,每个线程块有256个线程,但这并不意味着它们会立即执行,也就是说这256个线程并不会在同一时刻都被执行或完成执行。相反,GPU的执行硬件会用8个线程束来执行这些线程。
SIMT属于SIMD的范畴,因为它也是在多个数据上执行相同的指令。但是,SIMT允许由用户来分配线程,具体来说就是CUDA为每个线程指定了标识符(编号)。
一个关键的区别就是SIMD要求同一个向量中的所有元素要在一个统一的同步组中一起执行,而SIMT则允许属于同一个线程束的多个线程独立执行,这几个线程可以有不同的行为。因此SIMT允许线程级并发,也就是在统一线程束下的线程可以同时做不同的事情。
三个不同:
- 每个线程都有自己的指令地址计数器
- 每个线程都有自己的寄存器状态
- 每个线程可以有一个独立的执行路径
GPU架构
流式多处理器SM
一个线程块只能在一个SM上被调度,但一个SM可以对应多个线程块。
当SM指定了一个或多个要计算的线程块时,这些线程块会被分为多个warp,等待调度。
线程束中的线程都在不同的数据上执行相同的命令。
SM容纳线程块的数量,取决于SM内的共享内存和寄存器以及线程占用的资源。
线程块里的所有线程在逻辑上并行运行,但并不是所有的线程都可以同时在物理层面执行。(一个SM同时只调度一个warp,其余warp等待,不同的warp间的切换是零开销的因为warp的执行上下文在warp的整个生命周期都会被SM维护)
NVIDIA GeForce RTX 3090的Compute Capabilities是8.6,其中包含82个SM,每个SM中允许同时存在的最大线程数量为1536,求:理论上同一时刻并行执行线程数量为多少?并发执行线程数量为多少?
其中包含82个SM,每个SM中允许同时存在的最大线程数量为1536,即最多可以存在48个warp,由于warp是通过warp调度器并发执行,warp中32条线程是并行执行,因此笼统上可以认为,同一时刻并行执行线程数量为82*32=2624,并发执行线程数量为82*32*48=125952。
内存模型
| 存储器 | 位置 | 是否缓存 | 访问权限 | 生存周期 |
|---|---|---|---|---|
| 寄存器 | 片上 | 无 | device | 与线程、核函数相同 |
| 共享内存 | 片上 | 无 | device | 与block相同 |
| 本地内存 | 板载 | 无 | device | 与线程、核函数相同 |
| 全局内存 | 板载 | 无 | device&host | 程序 |
| 纹理内存、常量内存 | 板载 | 有 | device&host | 程序 |
定义在CUDA核函数中的变量,什么时候是寄存器变量,什么时候是本地变量呢?
以下三种情况是本地变量,其余则寄存器变量
- 编译阶段无法确定的数组
- 数组或结构体占用的空间很大
- 核函数中定义了很多的变量,寄存器装不下、
从寄存器溢出到本地内存的,本质上与全局内存在同一个存储区域


内存访问模式
全局内存通过缓存来实现加载/存储。所有对全局内存的访问都会通过L2 cache(一般128字节)。
对齐访问
第一个地址是缓存粒度(一般32字节)的偶数倍(cache line取数据开始位置就是如此)
合并访问
一个线程束中的全部线程访问一个连续的内存块。合并访问指的是线程束对全局内存的一次访问请求导致最少的数据传输(合并度=100%),否则是非合并访问。
5种访问方式,合并度的计算??
如果说读取和写入都不能合并访问,那么应该优先保证合并写入。只读数据的非合并访问,可以用__ldg()函数做缓存,也可以用共享内存转换为合并地。
共享内存与bank conflict
共享内存可以被程序员直接操控。
共享内存被划分为许多的banks.
- 一个warp中的所有线程访问同一bank同一地址-广播
- 一个warp中的不同线程访问一个bank的不同地址-bank conflict
- 多个线程访问同一bank同一地址-多播
Memory Padding 内存填充解决Bank confilct
Padding操作:在sData的第二维+1,即sData[BS][BS+1]
填充的部分不能用于数据存储,导致可用的共享内存数量减少。
代码
图像翻转CPU
多线程翻转图像,同时手动维护缓存。
void * MTFlipHM(void * tid){
struct Pixel pix; //temp swap pixel
int row, col;
int id = *((int *) tid);
int start = id * ip.Vpixels/NumThreads;
int end = start + ip.Vpixels/NumThreads;
unsigned char buffer[16384];
for (row = st ; row < ed; row++)
{
memcpy(buffer, TheImage[row], ip.Hbytes);
col = 0;
while (col < ip.Hpixels * 3 /2){
pix.B = buffer[col];
pix.G = buffer[col+1];
pix.R = buffer[col+2];
buffer[col] = buffer[ip.Hpixels*3 - col -3];
buffer[col+1] = buffer[ip.Hpixels*3 - col -2];
buffer[col+2] = buffer[ip.Hpixels*3 - col -1];
buffer[ip.Hpixels*3 - col -3] = pix.B;
buffer[ip.Hpixels*3 - col -2] = pix.G;
buffer[ip.Hpixels*3 - col -1] = pix.R;
col += 3;
}
}
memcpy(TheImage[row],buffer,ip.Hbytes);
pthread_exit(NULL);
}
void * MTFlipVM(void * tid){
struct Pixel pix; //temp swap pixel
int row, col;
int id = *((int *) tid);
int start = id * ip.Vpixels/NumThreads;
int end = start + ip.Vpixels/NumThreads;
unsigned char buffer1[16384], buffer2[16384];
for (row = start; row < end; row ++)
{
memcpy(buffer1,TheImage[row],ip.Hbytes);
int mirrow = ip.Vpixels - 1 - row;
memcpy(buffer2,TheImage[mirrow],ip.Hbytes);
// 再错位拷贝即完成交换
memcpy(TheImage[row],buffer2,ip.Hbytes);
memcpy(TheImage[mirrow],buffer1,ip.Hbytes);
}
}
pthread_create(&ThHandle[i], &ThAttr, MTFlipFunc, (void *)&ThParam[i]);
for(i=0; i<NumThreads; i++)
pthread_join(ThHandle[i], NULL);数组相加
const int a=1, b=2, c=3;
__global__ void add(double *x, double *y, double* z){
const int n = blockIdx.x * blockDim.x + threadIdx.x;
if (n<N) z[n] = x[n] + y[n];
}
int main(){
const int N = 1e9;
const int M = sizeof(double) * N;
double *h_x = (double*) malloc(M);
double *h_y = (double*) malloc(M);
double *h_z = (double*) malloc(M);
for (int i=0; i<N; i++)
{
h_x[i] = a;
h_y[i] = b;
}
double *d_x, *d_y, *d_z;
cudaMalloc((void**) &d_x, M);
cudaMalloc((void**) &d_y, M);
cudaMalloc((void**) &d_z, M);
const int block_size = 128;
int grid_size = (N+block_size-1) / block_size;
add<<<grid_size, block_size>>>(d_x, d_y, d_z);
cudaMemcpy(h_z, d_z, M, cudaMemcpyDeviceToHost);
free(h_x),free(h_y),free(h_z);
cudaFree(d_x),cudaFree(d_y),cudaFree(d_z);
}图像翻转
__global__ void Vflip(uch *ImgDst, uch *ImgSrc, ui Hpixels, ui Vpixels){
ui ThrPerBlk = blockDim.x;
ui MYbid = blockIdx.x;
ui MYtid = threadIdx.x;
ui MYgtid = ThrPerBlk * MYbid + MYtid;
ui BlkPerRow = (Hpixels + ThrPerBlk - 1) / ThrPerBlk; // ceil
ui RowBytes = (Hpixels * 3 + 3) & (~3);
ui MYrow = MYbid / BlkPerRow;
ui MYcol = MYgtid - MYrow*BlkPerRow*ThrPerBlk;
if (MYcol >= Hpixels) return;// col out of range
ui MYmirrorrow = Vpixels - 1 - MYrow;
ui MYsrcOffset = MYrow * RowBytes;
ui MYdstOffset = MYmirrorrow * RowBytes;
ui MYsrcIndex = MYsrcOffset + 3 * MYcol;
ui MYdstIndex = MYdstOffset + 3 * MYcol;
// swap pixels RGB @MYcol , @MYmirrorcol
ImgDst[MYdstIndex] = ImgSrc[MYsrcIndex];
ImgDst[MYdstIndex + 1] = ImgSrc[MYsrcIndex + 1];
ImgDst[MYdstIndex + 2] = ImgSrc[MYsrcIndex + 2];}
__global__ void Hflip(uch *ImgDst, uch *ImgSrc, ui Hpixels){
ui ThrPerBlk = blockDim.x;
ui MYbid = blockIdx.x;
ui MYtid = threadIdx.x;
ui MYgtid = ThrPerBlk * MYbid + MYtid;
ui BlkPerRow = (Hpixels + ThrPerBlk -1 ) / ThrPerBlk; // ceil
ui RowBytes = (Hpixels * 3 + 3) & (~3);
ui MYrow = MYbid / BlkPerRow;
ui MYcol = MYgtid - MYrow*BlkPerRow*ThrPerBlk;
if (MYcol >= Hpixels) return;// col out of range
ui MYmirrorcol = Hpixels - 1 - MYcol;
ui MYoffset = MYrow * RowBytes;
ui MYsrcIndex = MYoffset + 3 * MYcol;
ui MYdstIndex = MYoffset + 3 * MYmirrorcol;
// swap pixels RGB @MYcol , @MYmirrorcol
ImgDst[MYdstIndex] = ImgSrc[MYsrcIndex];
ImgDst[MYdstIndex + 1] = ImgSrc[MYsrcIndex + 1];
ImgDst[MYdstIndex + 2] = ImgSrc[MYsrcIndex + 2];}矩阵转置
__global__ void transpose(int a[], int b[], int N){
//分配共享内存
__shared__ int S[TILE][TILE + 1];
int bx = blockIdx.x * TILE;
int by = blockIdx.y * TILE;
int ix = bx + threadIdx.x;
int iy = by + threadIdx.y;
if (ix < N && iy < N)// 读入共享内存
S[threadIdx.y][threadIdx.x] = a[iy * N + ix];
__syncthreads();//同步,这是必不可少的
int ix2 = bx + threadIdx.y;
int iy2 = by + threadIdx.x;
if (ix2 <N && iy2 < N)// 写回
b[ix2 * N + iy2 ] = S[threadIdx.x][threadIdx.y];
}方阵相乘
__shared__ float Mds[WIDTH][TILE_WIDTH];
__shared__ float Nds[TILE_WIDTH][WIDTH];
int bx=blockIdx.x ; int by = blockIdx.y;
int tx=threadIdx.x ; int ty = threadIdx.y;
int Row = by *TILE_WIDTH +ty;
int Col = bx*TILE_WIDTH + tx;
float Pvalue = 0;
for(int m=0; m<WIDTH/TILE_WIDTH; ++m)
{
// 每个线程载入M的子矩阵的一个元素
Mds[ty][tx] = Md[Row*width+(m*TILE_WIDTH+tx)];
//每个线程载入N的子矩阵的一个元素
Nds[ty][tx] = Nd[(m*TILE_WIDTH+ty)*width+Col];
__syncthreads();
for (int k = 0; k < TILE_WIDTH; ++k)
Pvalue += Mds[ty][k] * Nds[k][tx];
__syncthreads();
}
Pd[Row*WIDTH+Col] = Pvalue;//将结果写回P矩阵直方图
#define SIZE (100*1024*1024)
//通过工具函数big_random_block()来生成随机的字节流
unsigned char *buffer =(unsigned char*)big_random_block( SIZE );
unsigned int histo[256];
for (int i = 0; i<256; i++)
histo[i] = 0;
for (int i = 0; i < SIZE; i++)
histo[buffer[i]]++;
long histoCount = 0;
for (int i = 0; i<256; i++) {
histoCount += histo[i]; }
__global__ void histo_kernel(unsigned char *buffer, long size, unsigned int *histo){
__shared__ unsigned int temp[256];
temp[threadIdx.x] = 0;
__syncthreads();
int i = threadIdx.x + blockIdx.x * blockDim.x;
int offset = blockDim.x *gridDim.x;
while (i<size){
atomicAdd(&temp[buffer[i]], 1);
i += offset;
}
__syncthreads();
atomicAdd(&(histo[threadIdx.x]), temp[threadIdx.x]);
}规约求和
规约求和与TOP K类似,下面的代码为官方代码,理解参考这篇文章
__global__ void _sum_gpu(int *input, int count, int *output)
{
__shared__ int sum_per_block[BLOCK_SIZE];
int temp = 0;
for (int idx = threadIdx.x + blockDim.x * blockIdx.x;
idx < count; idx += gridDim.x * blockDim.x
)
{// 跨网格循环,一个线程加多个数据,应对海量数据
temp += input[idx];
}
sum_per_block[threadIdx.x] = temp; //the per-thread partial sum is temp!
__syncthreads();
//**********shared memory summation stage***********
for (int length = BLOCK_SIZE / 2; length >= 1; length /= 2)
{
int double_kill = -1;
if (threadIdx.x < length)
{
double_kill = sum_per_block[threadIdx.x] + sum_per_block[threadIdx.x + length];
}
__syncthreads(); //why we need two __syncthreads() here, and,
if (threadIdx.x < length)
{
sum_per_block[threadIdx.x] = double_kill;
}
__syncthreads(); //....here ?
} //the per-block partial sum is sum_per_block[0]
if (blockDim.x * blockIdx.x < count) //in case that our users are naughty
{
//the final reduction performed by atomicAdd()
if (threadIdx.x == 0) atomicAdd(output, sum_per_block[0]);
}
}
TOP K
具体实现流程如下:
- 将数据复制到GPU显存中
float *d_data; cudaMemcpy(d_data, h_data, size, cudaMemcpyHostToDevice); - 将数据存储到二元组中
typedef struct { float value; int index; } Tuple; Tuple *d_tuples; int threadsPerBlock = 256; int blocksPerGrid = (n + threadsPerBlock - 1) / threadsPerBlock; initializeTuples<<<blocksPerGrid, threadsPerBlock>>>(d_data, d_tuples, n); ``` 3. 对二元组进行归约操作,得到前K个最大/最小值的索引 ```cpp int *d_indices; kReduceKernel<<<blocksPerGrid, threadsPerBlock>>>(d_tuples, d_indices, n, k); __global__ void kReduceKernel(Tuple *input, int *output, int n, int k) { extern __shared__ Tuple shared[]; int tid = threadIdx.x; int i = blockIdx.x * blockDim.x + threadIdx.x; shared[tid] = (i < n) ? input[i] : Tuple{0, 0}; __syncthreads(); for (int s = blockDim.x / 2; s > 0; s >>= 1) { if (tid < s) shared[tid] = (shared[tid].value > shared[tid + s].value) ? shared[tid] : shared[tid + s]; __syncthreads(); } if (tid == 0) output[blockIdx.x] = shared[0].index; } - 在CPU中恢复原始数据并按照索引排序,得到前K个最大/最小值
完成以上步骤后,就可以得到排序后的前K个最大/最小值了。cudaMemcpy(h_indices, d_indices, size, cudaMemcpyDeviceToHost); for (int i = 0; i < k; ++i) { int index = h_indices[i]; h_result[i] = h_data[index]; } std::sort(h_result, h_result + k);
实验
实验一:PI的三种求法、线程池
实验二:矩阵相乘、转置、规约、TOP K 问题
全局内存、共享内存优化、bank冲突优化
手写并行计算报告3-4页纸 cpu pi三种求法 生产者消费者模式 GPU 主程序流程明确一次即可,核函数不同,重点全局内存与共享内存实现, 矩阵相乘直方图(跨网格循环)规约100w数组中的最大值 报告在考试时上交
20级真题
简答题
Amdel定律,处理器n个,串行40%,求加速比极限。
给RGB图像680*480,分4个线程(没说怎么分),每个线程处理的像素范围和字节范围;
PPT线程束并行并发数量的例题原题;
NVIDIA GeForce RTX 3090的Compute Capabilities是8.6,其中包含82个SM,每个SM中允许同时存在的最大线程数量为1536,求:理论上同一时刻并行执行线程数量为多少?并发执行线程数量为多少?
其中包含82个SM,每个SM中允许同时存在的最大线程数量为1536,即最多可以存在48个warp,由于warp是通过warp调度器并发执行,warp中32条线程是并行执行,因此笼统上可以认为,同一时刻并行执行线程数量为82*32=2624,并发执行线程数量为82*32*48=125952。
矩阵转置过程的某个元素全局id;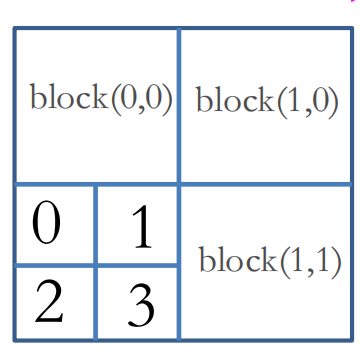
问元素3的全局id
可不可以一边复制数据,一边转置(CUDA流);
程序分析题
第一题,课堂练习原题;<4,4>改成了<5,5>;要说明过程;
第二题,少了原子操作的直方图规约,问有什么问题;
CPU编程
求数组a[2,1000000]中的素数,要求10个线程等分;
线程池伪代码:客户端、服务端(邮件功能、导出功能、流量统计等一堆功能);
GPU编程
全局内存的矩阵相乘;
向量a,b内积,维数=1024000000;定死blockdim.x = blockdim.y =16; 设计Grid;要求用共享内存优化、解决bank冲突、输出结果回到CPU做最终合并。
感受:非代码题宝宝巴士,代码题重拳出击,根本写不完。